We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心 是
是

 证明,也就是透过在两个集合间建立
证明,也就是透过在两个集合间建立 个
个
 (
(

 且映成
且映成 函数)来证明它们
函数)来证明它们 元素个数相等。
元素个数相等。
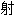 ,双
,双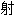
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心 是
是

 证明,也就是透过在两个集合间建立
证明,也就是透过在两个集合间建立 个
个
 (
(

 且映成
且映成 函数)来证明它们
函数)来证明它们 元素个数相等。
元素个数相等。
声明:以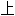

 、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件
、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心的是对射的证明,也就是透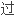


 集合间建立
集合间建立
 对射(
对射( 对
对 且映成的函数)来证明它们的
且映成的函数)来证明它们的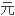

 数相等。
数相等。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经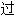 人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心的是对射的证明,也就是透过在两个集合间建立 个对射(
个对射( 对
对 且映成的函数)来证明它们的元素个数相等。
且映成的函数)来证明它们的元素个数相等。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审 ,
,
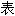 达内容亦不代
达内容亦不代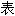 本软件的观点;若发现问题,欢迎向我们指正。
本软件的观点;若发现问题,欢迎向我们指正。

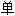
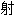 ,双
,双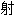
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心的是对 的证明,也就是透过在两个集合间建立
的证明,也就是透过在两个集合间建立 个对
个对 (
( 对
对 且映成的函数)来证明它们的元素个数相等。
且映成的函数)来证明它们的元素个数相等。
声明:以上例句、词性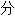 类均由互联网资源自动生成,
类均由互联网资源自动生成,
 经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎
经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎 我们指正。
我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关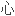

 对射
对射 证明,也就
证明,也就 透过在两个集合间建立
透过在两个集合间建立 个对射(
个对射( 对
对 且映成
且映成 函数)来证明它们
函数)来证明它们 元素个数相等。
元素个数相等。
声明:以上例句、词
 类均由互联网资源自动生成,部
类均由互联网资源自动生成,部 未经过人工审核,其表达内容亦不代表本软件
未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心的是 射的证明,也就是透过在两个集合间建立
射的证明,也就是透过在两个集合间建立 个
个 射(
射(



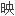 成的函数)来证明它们的元素个数相等。
成的函数)来证明它们的元素个数相等。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心的是对射的证明,也就是透过在两个集合间建立 个对射(
个对射( 对
对 且映成的函数)来证明它们的元素个数相等。
且映成的函数)来证明它们的元素个数相等。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人

 ,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
我们主要关心

 射
射 证明,也就
证明,也就 透过在两个集合间建立
透过在两个集合间建立 个
个 射(
射(

 且映成
且映成 函数)来证明它们
函数)来证明它们 元素个数相等。
元素个数相等。
声明:以上例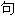 、词
、词 分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件
分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
We will be concerned primarily with bijective proofs, i.e., showing that two sets have the same number of elements by exhibiting a bijection (one-to-one correspondence) between them.
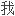
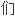
 要关心的是对射的证明,也就是透过在两个集合间建立
要关心的是对射的证明,也就是透过在两个集合间建立 个对射(
个对射( 对
对 且映成的函数)来证明它
且映成的函数)来证明它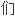 的元素个数相等。
的元素个数相等。
声明:以上例句、词性分类均
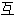
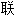 网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向
网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向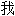
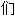 指正。
指正。