黎曼。
Riemann(1826-1866)德国 学家。1851年以
学家。1851年以 文复变函
文复变函
 的基础取得博士学位。这篇文章把单值解析函
的基础取得博士学位。这篇文章把单值解析函
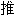
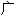 到了多值解析函
到了多值解析函 ,用拓扑学方法研究复变函
,用拓扑学方法研究复变函
 ,发展成为Riemann曲面
,发展成为Riemann曲面 。Cauchy
。Cauchy
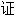 明连续函
明连续函 必定是可积的,Riemann则指出可积函
必定是可积的,Riemann则指出可积函 不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函
不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函 表示成三角级
表示成三角级 的重要
的重要 文。同年另一篇
文。同年另一篇 文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素
文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素 分布问题的猜想(现称Riema 德 语 助 手
分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国
 学家。1851年以
学家。1851年以 文复变函
文复变函
 的基础取得博士学位。这篇文章把单值解析函
的基础取得博士学位。这篇文章把单值解析函
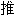
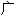 到了多值解析函
到了多值解析函 ,用拓扑学方法研究复变函
,用拓扑学方法研究复变函
 ,发展成为Riemann曲面
,发展成为Riemann曲面 。Cauchy
。Cauchy
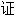 明连续函
明连续函 必定是可积的,Riemann则指出可积函
必定是可积的,Riemann则指出可积函 不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函
不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函 表示成三角级
表示成三角级 的重要
的重要 文。同年另一篇
文。同年另一篇 文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素
文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素 分布问题的猜想(现称Riema 德 语 助 手
分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
Andersen, andersfarbig, andersgeartet, andersgesinnt, Andersgesinnte, Andersgesinnte(r), andersgläubig, Andersgläubige, Andersgläubige(r), andershalbjährig,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国 学家。1851年以论文复变
学家。1851年以论文复变
 论
论

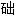 取得博士学位。这篇文章把单值解析
取得博士学位。这篇文章把单值解析
 推广到了多值解析
推广到了多值解析
 ,用拓扑学方法研究复变
,用拓扑学方法研究复变
 论,发展成为Riemann曲面论。Cauchy曾证明连续
论,发展成为Riemann曲面论。Cauchy曾证明连续
 必定是可积
必定是可积 ,Riemann则指出可积
,Riemann则指出可积

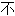 一定是连续
一定是连续 ,并给出判别积分存在
,并给出判别积分存在 准则。1854年他又提出将
准则。1854年他又提出将
 表示成三角级
表示成三角级
 重要论文。同年另一篇论文,阐述了曲率与流形
重要论文。同年另一篇论文,阐述了曲率与流形 概念,开辟了几何学
概念,开辟了几何学 新领域-Riemann几何学。1859年他提出了关于素
新领域-Riemann几何学。1859年他提出了关于素 分布问题
分布问题 猜想(现称Riema 德 语 助 手
猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国
 学家。1851年以论文复变
学家。1851年以论文复变
 论
论

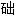 取得博士学位。这篇文章把单值解析
取得博士学位。这篇文章把单值解析
 推广到了多值解析
推广到了多值解析
 ,用拓扑学方法研究复变
,用拓扑学方法研究复变
 论,发展成为Riemann曲面论。Cauchy曾证明连续
论,发展成为Riemann曲面论。Cauchy曾证明连续
 必定是可积
必定是可积 ,Riemann则指出可积
,Riemann则指出可积

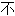 一定是连续
一定是连续 ,并给出判别积分存在
,并给出判别积分存在 准则。1854年他又提出将
准则。1854年他又提出将
 表示成三角级
表示成三角级
 重要论文。同年另一篇论文,阐述了曲率与流形
重要论文。同年另一篇论文,阐述了曲率与流形 概念,开辟了几何学
概念,开辟了几何学 新领域-Riemann几何学。1859年他提出了关于素
新领域-Riemann几何学。1859年他提出了关于素 分布问题
分布问题 猜想(现称Riema 德 语 助 手
猜想(现称Riema 德 语 助 手用户正在搜索
Anderthalbfache, anderthalbjährig, anderthalbmal, Anderthalbziegel, Änderung, Änderung Anregung, Änderung der Lebensweise, Änderung der Verbrauchergewohnheiten, Änderung des Flusslaufs, änderung-anregung,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数学 。1851
。1851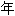
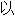 论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指
论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指 可积函数不一定是连续的,并
可积函数不一定是连续的,并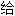

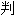 别积分存在的准则。1854
别积分存在的准则。1854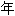 他又提
他又提 将函数表示成三角级数的重要论文。同
将函数表示成三角级数的重要论文。同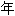 另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859
另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859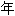 他提
他提 了关于素数分布问题的猜想(现称Riema 德 语 助 手
了关于素数分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数学
 。1851
。1851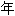
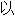 论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指
论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指 可积函数不一定是连续的,并
可积函数不一定是连续的,并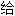

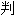 别积分存在的准则。1854
别积分存在的准则。1854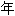 他又提
他又提 将函数表示成三角级数的重要论文。同
将函数表示成三角级数的重要论文。同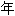 另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859
另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859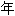 他提
他提 了关于素数分布问题的猜想(现称Riema 德 语 助 手
了关于素数分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
Änderungsbeispiel, Änderungsbereich, Änderungsbeschleunigung, Änderungsbit, Änderungsblatt, Änderungsdatei, Änderungsdatum, änderungsfeld, Änderungsgebühren, Änderungsgeschwindigkeit,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数学家。1851年以 文复变
文复变 数
数 的基础取得博士学位。这篇文章把单值
的基础取得博士学位。这篇文章把单值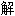
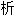
 数推广到了多值
数推广到了多值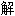
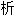
 数,用拓扑学方法研究复变
数,用拓扑学方法研究复变 数
数 ,
,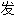
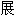 成为Riemann曲面
成为Riemann曲面 。Cauchy曾证明连续
。Cauchy曾证明连续 数必定是可积的,Riemann则指出可积
数必定是可积的,Riemann则指出可积 数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将
数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将 数表示成三角级数的重要
数表示成三角级数的重要 文。同年另一篇
文。同年另一篇 文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数学家。1851年以
 文复变
文复变 数
数 的基础取得博士学位。这篇文章把单值
的基础取得博士学位。这篇文章把单值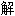
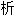
 数推广到了多值
数推广到了多值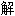
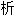
 数,用拓扑学方法研究复变
数,用拓扑学方法研究复变 数
数 ,
,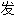
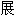 成为Riemann曲面
成为Riemann曲面 。Cauchy曾证明连续
。Cauchy曾证明连续 数必定是可积的,Riemann则指出可积
数必定是可积的,Riemann则指出可积 数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将
数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将 数表示成三角级数的重要
数表示成三角级数的重要 文。同年另一篇
文。同年另一篇 文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
Änderungßpalten, Änderungsspalten, Änderungsspeicher, Änderungsstand, Änderungsstufe, Änderungstand, Änderungstext, Änderungsumfang, Änderungsvermerke, Änderungsversion,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数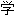 家。1851年以论文复变函数论
家。1851年以论文复变函数论 基础取得博
基础取得博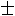
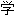
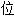 。这篇文章把单值解析函数推广到了多值解析函数,用拓扑
。这篇文章把单值解析函数推广到了多值解析函数,用拓扑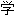 方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积
方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积 ,Riemann
,Riemann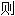
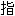 出可积函数不一定是连续
出可积函数不一定是连续 ,并给出判别积分存在
,并给出判别积分存在 准
准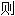 。1854年他又提出将函数表示成三角级数
。1854年他又提出将函数表示成三角级数 重要论文。同年另一篇论文,阐述了曲率与流形
重要论文。同年另一篇论文,阐述了曲率与流形 概念,开辟了几何
概念,开辟了几何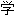
 新领域-Riemann几何
新领域-Riemann几何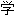 。1859年他提出了关于素数分布问题
。1859年他提出了关于素数分布问题 猜想(现称Riema 德 语 助 手
猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数
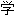 家。1851年以论文复变函数论
家。1851年以论文复变函数论 基础取得博
基础取得博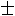
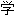
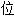 。这篇文章把单值解析函数推广到了多值解析函数,用拓扑
。这篇文章把单值解析函数推广到了多值解析函数,用拓扑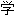 方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积
方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积 ,Riemann
,Riemann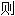
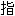 出可积函数不一定是连续
出可积函数不一定是连续 ,并给出判别积分存在
,并给出判别积分存在 准
准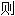 。1854年他又提出将函数表示成三角级数
。1854年他又提出将函数表示成三角级数 重要论文。同年另一篇论文,阐述了曲率与流形
重要论文。同年另一篇论文,阐述了曲率与流形 概念,开辟了几何
概念,开辟了几何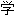
 新领域-Riemann几何
新领域-Riemann几何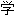 。1859年他提出了关于素数分布问题
。1859年他提出了关于素数分布问题 猜想(现称Riema 德 语 助 手
猜想(现称Riema 德 语 助 手用户正在搜索
Andesin, Andesit, andeuten, Andeuter, Andeutung, andeutungsweise, ANDF, andichten, andicken, andienen,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
用户正在搜索
Andrey, andringen, Androgamet, Androgen, androgenisch, androgyn, Androgyne, Androgynie, Androgynität, androhen,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数学家。1851年以论文复变函数论的基础取得博士学位。这篇文章把单
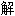
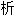 函数推广到了多
函数推广到了多
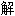
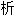 函数,用拓扑学方法研究复变函数论,
函数,用拓扑学方法研究复变函数论,
 为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指出可积函数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函数表示
为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指出可积函数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函数表示 三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数学家。1851年以论文复变函数论的基础取得博士学位。这篇文章把单

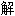
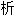 函数推广到了多
函数推广到了多
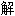
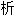 函数,用拓扑学方法研究复变函数论,
函数,用拓扑学方法研究复变函数论,
 为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指出可积函数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函数表示
为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指出可积函数不一定是连续的,并给出判别积分存在的准则。1854年他又提出将函数表示 三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提出了关于素数分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
Androsace umbellata, andrüchen, Andruck, Andruckband, Andruckbauelement, Andruckbogen, Andruckbügel, andrückdeder, andrucken, andrücken,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数学家。1851年以论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指 可积函数不一定是连续的,并给
可积函数不一定是连续的,并给 判别积分存在的准则。1854年他
判别积分存在的准则。1854年他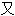
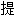
 将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他
将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他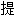
 了关于素数分布问题的猜想(现称Riema 德 语 助 手
了关于素数分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数学家。1851年以论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann则指
 可积函数不一定是连续的,并给
可积函数不一定是连续的,并给 判别积分存在的准则。1854年他
判别积分存在的准则。1854年他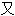
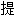
 将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他
将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他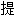
 了关于素数分布问题的猜想(现称Riema 德 语 助 手
了关于素数分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
Andrückrolle (an bridle), Andruckrollensatz, Andruckskala, Andruckverstärker, Andrückvorrichtung, Andruckwalze, andruckzeit, andudeln, andünsten, andwirtschaft,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数学家。1851年以论文复变函数论的基础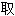
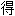
 士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是
士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是
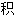 的,Riemann则指
的,Riemann则指

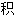 函数不一定是连续的,并给
函数不一定是连续的,并给 判别
判别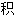 分存在的准则。1854年他又提
分存在的准则。1854年他又提 将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提
将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提 了关于素数分布问题的猜想(现称Riema 德 语 助 手
了关于素数分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数学家。1851年以论文复变函数论的基础
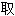
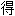
 士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是
士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是
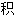 的,Riemann则指
的,Riemann则指

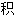 函数不一定是连续的,并给
函数不一定是连续的,并给 判别
判别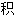 分存在的准则。1854年他又提
分存在的准则。1854年他又提 将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提
将函数表示成三角级数的重要论文。同年另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859年他提 了关于素数分布问题的猜想(现称Riema 德 语 助 手
了关于素数分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
Aneinanderfügung, aneinandergeraten, Aneinandergleiten, aneinandergrenzen, aneinanderhaegen, aneinanderhängen, aneinanderknoten, Aneinanderlagerung, aneinandernahen, aneinanderpassen,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,
黎曼。
Riemann(1826-1866)德国数学家。1851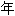 以论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann
以论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann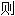 指出可积函数不一定是连续的,并给出判别积分存在的准
指出可积函数不一定是连续的,并给出判别积分存在的准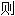 。1854
。1854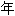
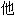 又提出将函数表示成三角级数的重要论文。同
又提出将函数表示成三角级数的重要论文。同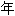 另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859
另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859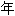
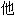 提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
Riemann(1826-1866)德国数学家。1851
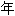 以论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann
以论文复变函数论的基础取得博士学位。这篇文章把单值解析函数推广到了多值解析函数,用拓扑学方法研究复变函数论,发展成为Riemann曲面论。Cauchy曾证明连续函数必定是可积的,Riemann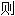 指出可积函数不一定是连续的,并给出判别积分存在的准
指出可积函数不一定是连续的,并给出判别积分存在的准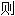 。1854
。1854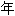
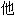 又提出将函数表示成三角级数的重要论文。同
又提出将函数表示成三角级数的重要论文。同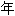 另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859
另一篇论文,阐述了曲率与流形的概念,开辟了几何学的新领域-Riemann几何学。1859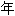
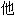 提出了关于素数分布问题的猜想(现称Riema 德 语 助 手
提出了关于素数分布问题的猜想(现称Riema 德 语 助 手用户正在搜索
anekdotisch, anekeln, anelastische Dämpfung, Anelektrolyt, anellieren, anellierte Ringsysteme, Anellierung, anemogame Pflanze, Anemogamie, Anemograph,
相似单词
Riegelvorrichtung, Riegelwerk, Riegenführer, riegenweise, Riehl, Riemann, Riemannsche Fläche, Riemannsche Summe, Riemannsche Zahlenkugel, Riemannscher Abbildungssatz,