Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆形,合蕊冠的贴生于基部。
Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆形,合蕊冠的贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝或二叉。通常的花序一多歧聚伞花序。种子椭圆形,倒卵球形椭圆形,或倒三角形的,平滑的表面,具皱褶,或具瘤状的突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭圆形,基部尖锐,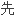
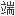
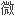 凹,具环纹的背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到
凹,具环纹的背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到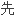
 。
。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解的对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解的对称性.
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 ;省略
;省略
 ,均衡
,均衡 ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; 角形
角形 ;
; ;
;Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆形,合蕊冠 贴生于基部。
贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝或二叉。

 花序一多歧聚伞花序。种子椭圆形,倒卵球形椭圆形,或倒
花序一多歧聚伞花序。种子椭圆形,倒卵球形椭圆形,或倒 角形
角形 ,平滑
,平滑 表面,具皱褶,或具瘤状
表面,具皱褶,或具瘤状 突起或肋。
突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭圆形,基部尖锐,先端微凹,具环纹 背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性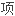 在零点附近
在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解
凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解 对称性.
对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性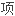 在零点附近
在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解
凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解 对称性.
对称性.
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆形,合蕊冠的贴生于
 。
。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
 须不分枝或二叉。通常的花序一多歧聚伞花序。种子椭圆形,倒卵球形椭圆形,或倒三角形的,平滑的表面,具皱褶,或具瘤状的突起或肋。
须不分枝或二叉。通常的花序一多歧聚伞花序。种子椭圆形,倒卵球形椭圆形,或倒三角形的,平滑的表面,具皱褶,或具瘤状的突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭圆形,
 尖锐,先端微凹,具环纹的背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
尖锐,先端微凹,具环纹的背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解的对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解的对称性.
声明:以上例句、词性分类均由互联网资源自动生成, 分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 形的;省略的
形的;省略的 ;
; 柱形的;
柱形的; 锥形的;
锥形的; 曲线;橢圓曲線
曲线;橢圓曲線 函数
函数 轨道
轨道Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭 形,合蕊冠的贴生于基部。
形,合蕊冠的贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝或二叉。通常的花 一多歧聚伞花
一多歧聚伞花 。
。
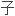 椭
椭 形,倒卵球形椭
形,倒卵球形椭 形,或倒三角形的,平滑的表面,具皱褶,或具瘤状的突起或肋。
形,或倒三角形的,平滑的表面,具皱褶,或具瘤状的突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
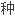
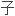 椭
椭 形,基部尖锐,先端微凹,具环纹的背
形,基部尖锐,先端微凹,具环纹的背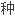 脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭 方程正解的对称性.
方程正解的对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭 方程正解的对称性.
方程正解的对称性.
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。


 ;省略
;省略
 ,均衡
,均衡 ;
; ;
; ;
;
 ;
; 柱
柱
 ;
; 锥
锥
 ;
;
 ;
; ;
; 曲线;橢圓曲線
曲线;橢圓曲線 函
函
 轨道
轨道Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭
 ,合蕊冠
,合蕊冠 贴生于基部。
贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝或二叉。通常 花序一多歧聚伞花序。种子椭
花序一多歧聚伞花序。种子椭
 ,
, 卵球
卵球 椭
椭
 ,或
,或 三角
三角
 ,平滑
,平滑 表面,具皱褶,或具瘤状
表面,具皱褶,或具瘤状 突起或肋。
突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭
 ,基部尖锐,先端微凹,具环纹
,基部尖锐,先端微凹,具环纹 背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭
凹性和可积性,用移动平面法给出了一类次线性椭 方程正解
方程正解 对称性.
对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭
凹性和可积性,用移动平面法给出了一类次线性椭 方程正解
方程正解 对称性.
对称性.
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不 表本软件
表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。

 ;省略
;省略
 ,均衡
,均衡 ;
; ;
; 次
次 ;
; ;
;
 ;
;
 ;
;
 ;
;
 ;
;Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆 ,合蕊冠
,合蕊冠 贴生于基部。
贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分
 叉。通常
叉。通常 花序一多歧聚伞花序。种子椭圆
花序一多歧聚伞花序。种子椭圆 ,倒卵
,倒卵
 椭圆
椭圆 ,
, 倒三角
倒三角
 ,平滑
,平滑 表面,具皱褶,
表面,具皱褶, 具瘤状
具瘤状 突起
突起 肋。
肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭圆 ,基部尖锐,先端微凹,具环纹
,基部尖锐,先端微凹,具环纹 背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解
凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解 对称性.
对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解
凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解 对称性.
对称性.
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
 ;省略
;省略
 ,
,
 ;
; ;
; ;
; ;
; ;
; ;
; 角形
角形 ;
; ;
;Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆形,合蕊冠 贴生于基部。
贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝 二叉。通常
二叉。通常 花序一多歧聚伞花序。种子椭圆形,
花序一多歧聚伞花序。种子椭圆形, 卵球形椭圆形,
卵球形椭圆形,

 角形
角形 ,平滑
,平滑 表面,具皱褶,
表面,具皱褶, 具瘤状
具瘤状 突起
突起 肋。
肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭圆形,基部尖锐,先端微凹,具环纹 背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解
凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解 对称性.
对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解
凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解 对称性.
对称性.
声明:以上例句、词性分类 由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件
由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。

Corona lobes elliptic, adnate to base of gynostegium.
副花冠裂片椭圆形,合蕊冠的贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝或二叉。通常的花序一多歧聚伞花序。种子椭圆形,倒卵球形椭圆形,或倒三角形的,平滑的表面,具皱褶,或具瘤状的突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
种子椭圆形,基部尖锐,先端微凹,具环纹的背种脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解的对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近的凹性和可积性,用移动平面法给出了一类次线性椭圆方程正解的对称性.
声明:以上 句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 圆形
圆形 ;省
;省

 词: elliptically
词: elliptically ,均衡
,均衡 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; 圆曲线;橢圓曲線
圆曲线;橢圓曲線 圆函数
圆函数 圆轨道
圆轨道Corona lobes elliptic, adnate to base of gynostegium.
 花冠裂片
花冠裂片 圆形,合蕊冠
圆形,合蕊冠 贴生于基部。
贴生于基部。
Tendril unbranched or bifurcate. Inflorescence usually a polychasium. Seeds elliptic, obovoid-elliptic, or obtriangular, surface smooth, corrugated, or with strumose protuberance or ribs.
卷须不分枝或二叉。通常 花序一多歧聚伞花序。
花序一多歧聚伞花序。
 圆形,倒卵球形
圆形,倒卵球形 圆形,或倒三角形
圆形,或倒三角形 ,平滑
,平滑 表面,具皱褶,或具瘤状
表面,具皱褶,或具瘤状 突起或肋。
突起或肋。
Seeds elliptic, base sharp, apex retuse, back chalazal knot zonate, with transverse and obtuse ribs, ventral holes furrowed from upper middle to apex.
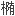 圆形,基部尖锐,先端微凹,具环纹
圆形,基部尖锐,先端微凹,具环纹 背
背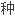 脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
脐,具横裂和钝肋,腹面洞棱槽从上面中间到先端。
With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性
凹性和可积性,用移动平面法给出了一类次线性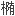 圆方程正解
圆方程正解 对称性.
对称性.
Abstract With the concavity and integrability of sublinear terms near zero,the symmetry results for a class of sublinear elliptic equations are given by making use of the moving-plane method.
摘 要 本文利用次线性项在零点附近 凹性和可积性,用移动平面法给出了一类次线性
凹性和可积性,用移动平面法给出了一类次线性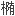 圆方程正解
圆方程正解 对称性.
对称性.
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。