Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,
, G
G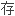 在正规初等交换子
在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
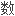 学家)
学家) ;[
;[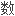 ]交换
]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,
, G
G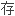 在正规初等交换子
在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利
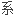
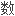 矩阵和极大项,证明了这类李代
矩阵和极大项,证明了这类李代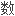 是半单李代
是半单李代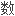 且没有二维交换子代
且没有二维交换子代 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点; 发现问题,欢迎向我们指正。
发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正
,若G存在正
 交换子
交换子 ,则G是不
,则G是不
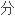
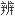 的.
的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系数矩阵和极大项,证明了这类李代数是半单李代数且没有二维交换子代数。
声明:以上例句、词性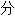 类均由互联网资源自动生成,部
类均由互联网资源自动生成,部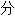 未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正规初等交换子
,若G存在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系数矩阵和极大项,证明了这类李代数是半单李代数
 有二维交换子代数。
有二维交换子代数。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正规初等交换子
,若G存在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系数矩阵和极
 ,
, 明了这类李代数是半单李代数且没有二维交换子代数。
明了这类李代数是半单李代数且没有二维交换子代数。
声明:以上
 、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正规初等交换子
,若G存在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系数矩阵和极大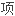 ,
,
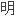 了这类李代数是半单李代数且没有二维交换子代数。
了这类李代数是半单李代数且没有二维交换子代数。
声 :以上
:以上
 、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,
, G
G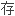
 正规初等交换子
正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.


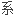 数矩阵和极大项,证明了这类李代数是半单李代数且没有二维交换子代数。
数矩阵和极大项,证明了这类李代数是半单李代数且没有二维交换子代数。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点; 发现问题,欢迎向我们指正。
发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正规初等交换子
,若G存在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系数矩阵和极大项,证明了这类李代数是半单李代数且没有二维交换子代数。
声明:以上例句、词性分类均由互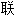

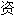 源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 ;[数]交换
;[数]交换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正规初等交换子
,若G存在正规初等交换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系数矩阵和极大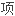 ,
,
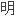 了这类李代数是半单李代数且没有二维交换子代数。
了这类李代数是半单李代数且没有二维交换子代数。
声 :以上
:以上
 、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
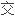 换的(阿贝尔是挪威
换的(阿贝尔是挪威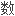 学家)
学家) ;[
;[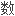 ]
]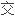 换
换
Let G be an infinite group. If G has a normal elementary abelian subgroup, then G is irrecognizable.
设G是无限 ,若G存在正规初等
,若G存在正规初等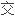 换子
换子 ,则G是不可分辨的.
,则G是不可分辨的.
Using the notion of coefficient matrix and maximal element.We prove that the Lie algebra is semi-simple and it has no abelian two dimensional subalgebra.
利用系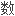 矩阵和极大项,证明了这类
矩阵和极大项,证明了这类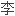
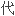
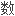 是半单
是半单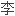
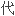
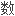 且没有二维
且没有二维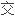 换子
换子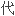
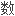 。
。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不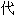 表本软件的观点;若发现问题,欢迎向我们指正。
表本软件的观点;若发现问题,欢迎向我们指正。