Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力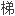
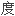 为重力位的二阶导数,可以通过星载
为重力位的二阶导数,可以通过星载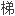
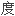
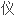 进行观测。
进行观测。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力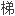
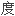 为重力位的二阶导数,可以通过星载
为重力位的二阶导数,可以通过星载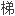
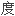
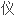 进行观测。
进行观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们利用Schwarz 导数极值集的重要性质部分的解决了几类平行四边 的单叶性内径。
的单叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中的一阶导数代换对
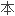 方程进行了简化处理,
方程进行了简化处理,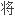

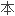 的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁的大挠
的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁的大挠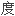 问题。
问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表 软件的观点;若发现问题,欢迎向我们指正。
软件的观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位的二阶导数,可以通过星载梯度仪进行观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们利用Schwarz 导数极值集的重要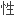
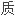

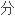 的解决了几类平行四边
的解决了几类平行四边 的单叶
的单叶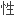 内径。
内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线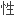
 方法中的一阶导数代换对基本方程进行了简化处理,将基本的微
方法中的一阶导数代换对基本方程进行了简化处理,将基本的微 积
积 方程转化为非线
方程转化为非线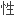 代数方程组,并结合双参数摄动研究了悬臂梁的大挠度问题。
代数方程组,并结合双参数摄动研究了悬臂梁的大挠度问题。
声明:以上例句、词
 类均由互联网资源自动生成,
类均由互联网资源自动生成,
 未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位 二阶导数,可以通过星载梯度仪进行观测。
二阶导数,可以通过星载梯度仪进行观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们利用Schwarz 导数极值集 重要性质部分
重要性质部分 解决了几类平行
解决了几类平行
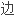


 叶性内径。
叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中 一阶导数代换对基本方程进行了简化处理,将基本
一阶导数代换对基本方程进行了简化处理,将基本 微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁
微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁 大挠度问题。
大挠度问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位的二阶导数,可以通过星载梯度仪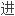
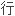 观测。
观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在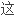

 中我们利用Schwarz 导数极值集的重要性质部分的解决了几类平
中我们利用Schwarz 导数极值集的重要性质部分的解决了几类平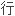 四边
四边 的单叶性内径。
的单叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中的 阶导数代换对基本方
阶导数代换对基本方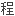
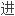
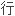 了简化处理,将基本的微分积分方
了简化处理,将基本的微分积分方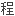 转化为非线性代数方
转化为非线性代数方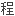 组,并结合双参数摄动研究了悬臂梁的大挠度问题。
组,并结合双参数摄动研究了悬臂梁的大挠度问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位的二阶导数,可以通过星载梯度仪进行观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们 用Schwarz 导数极值集的重要性质部分的解决
用Schwarz 导数极值集的重要性质部分的解决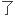
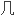
 平行四边
平行四边 的单叶性
的单叶性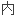
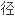 。
。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
 用拟线性分析方法中的一阶导数代换对基本方程进行
用拟线性分析方法中的一阶导数代换对基本方程进行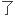 简化处理,将基本的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究
简化处理,将基本的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究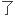 悬臂梁的大挠度问题。
悬臂梁的大挠度问题。
声明:以上例句、词性分 均由互联网资源自动生成,部分未经过人工审核,其表达
均由互联网资源自动生成,部分未经过人工审核,其表达 容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位的二阶导数,可以通过星载梯度仪进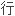
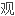
 。
。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们利用Schwarz 导数极值集的重要性质部分的解决了几类平 四边
四边 的单叶性内径。
的单叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中的一阶导数代换对基本方程进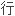 了
了
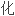
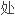 理,将基本的微分积分方程转
理,将基本的微分积分方程转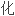 为非线性代数方程组,并结合双参数摄动研究了悬臂梁的大挠度问题。
为非线性代数方程组,并结合双参数摄动研究了悬臂梁的大挠度问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的 点;若发现问题,欢迎向我们指正。
点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位 二
二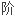 导数,可以通过星载梯度仪进行观测。
导数,可以通过星载梯度仪进行观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这 章中我们利用Schwarz 导数极
章中我们利用Schwarz 导数极

 重要性质部分
重要性质部分 解决了几类平行四边
解决了几类平行四边
 单叶性内径。
单叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中

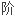 导数代换对基本方程进行了简化处理,将基本
导数代换对基本方程进行了简化处理,将基本 微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁
微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁 大挠度问题。
大挠度问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件 观点;若发现问题,欢迎向我们指正。
观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位的二阶导数,可以通过星载梯度仪进行观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们利用Schwarz 导数极值集的重要性质部分的解决 几类平行四边
几类平行四边 的单叶性内径。
的单叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中的一阶导数代换对基本方程进行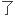 简化处理,将基本的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究
简化处理,将基本的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究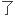

 梁的大挠度问题。
梁的大挠度问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
Gravity gradient is the second order derivative of gravitational potential, which can be observed by satellite gradiometer.
摘要重力梯度为重力位的二阶导数,可以通过星载梯度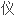
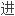
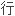 观测。
观测。
In this chapter, we partially solve the problem of inner radius of univalence for some parallelogram, applying the properties of extremal sets of Schwarz derivatives.
在这一章中我们利用Schwarz 导数极值集的重要性质部分的解决了几类平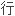 四边
四边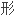 的单叶性内径。
的单叶性内径。
The large deflection problem of cantilever beams was studied by means of the biparametric perturbation method and the first order derivative substitution from pseudolinear analysis approach.
利用拟线性分析方法中的一阶导数代换对基本方程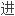
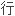 了简化
了简化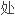
 ,
,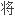 基本的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁的大挠度问题。
基本的微分积分方程转化为非线性代数方程组,并结合双参数摄动研究了悬臂梁的大挠度问题。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。